Part 1: Cryptography and Block Cipher Modes

I have a habit of spending some of my free time diving into topics that I stumble upon while browsing online. This time, it’s AES encryption with GCM mode, simply referred to as AES-GCM. It’s been a while since I’ve delved into the topic of cryptography, mostly because it’s not something I work with day-to-day as a developer, but also because the subject of “cryptography” intimidates me a bit. Fortunately, this topic turned out to be quite fun, and I wanted to write about it.

In this first post, I cover some of the basic cryptography concepts and the block cipher modes of operation. In Part 2: AES-GCM and AWS KMS, I cover AES and AES-GCM from a developer’s perspective, what role services like AWS KMS plays, and show code examples that work on Node.js.

The goal isn’t to understand the internal mechanisms of AES and AES-GCM but to understand why it’s so widely used, why we use a certain mode over another, why the crypto APIs are designed the way they are, and how we can use them effectively.

Foundations

Key-based Cryptography

A cryptographic algorithm, simply called a cipher, is a mathematical function used to encrypt and decrypt data. Encryption and decryption use related operations, often the inverse steps of the same algorithm. Modern ciphers do not rely on hiding the algorithm itself; instead, their security depends entirely on the strength and secrecy of the key. This means the algorithm can be publicly known without weakening the security of your encrypted data—as long as the key is unpredictable and kept secret. This principle is known as Kerckhoffs’s principle.

Symmetric vs. Asymmetric Algorithms

There are two types of key-based algorithms: symmetric and asymmetric.
In symmetric algorithms, the encryption key can be derived from the decryption key and vice versa. In AES and most symmetric algorithms today, the encryption and decryption keys are simply the same value.

In asymmetric algorithms, as you might have already guessed, the encryption key is different from the decryption key and cannot be derived from it. The encryption key is called the public key, while the decryption key is called the private key. Anyone with the public key can encrypt data, but only the holder of the private key can decrypt it. For example, with RSA, a sender encrypts a message using your public key, and only you, using your private key, can decrypt it.

Although both rely on keys and perform data encryption, they serve different purposes in modern systems:

• Speed: Symmetric algorithms (like AES) are extremely fast and suitable for encrypting large amounts of data. Asymmetric algorithms (like RSA or ECC) are much slower and used only for encrypting small pieces of data—usually keys, not full messages.

• Key Management: Symmetric encryption requires both parties to share the same secret key, which makes secure key distribution a challenge. Asymmetric encryption avoids this problem because the public key can be shared freely.

• Use Cases: Symmetric ciphers are used for bulk data encryption, file encryption, TLS session encryption, VPNs. Asymmetric ciphers are used for key exchange, digital signatures, certificate validation, establishing trust.

• Security Model: Symmetric relies on keeping one key secret. Asymmetric relies on keeping the private key secret while the public key can be openly distributed.

Because each has strengths and weaknesses, real-world systems combine them. For example, TLS uses asymmetric encryption to securely exchange a symmetric session key, and then uses AES to encrypt the actual data.

Stream Ciphers vs. Block Ciphers

Symmetric ciphers can be further categorised into two types. Algorithms that operate on data one bit or byte at a time are called stream ciphers, while algorithms that operate on fixed-size groups of bits called blocks are known as block ciphers. Modern block sizes are typically 64 bits (8 bytes) or 128 bits (16 bytes). While this distinction seems important, it becomes less rigid in practice because block ciphers can operate in modes that effectively behave like stream ciphers.

XOR Bitwise Operator

Before diving into block cipher modes, it’s important to understand one operation that shows up everywhere in modern symmetric cryptography: XOR (exclusive OR). It’s a simple bitwise operator, but it plays a foundational role in how encryption mixes data.

XOR compares two bits and returns 1 if they differ, and 0 if they are the same:

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

There are two key properties that make XOR so useful in cryptography:

1. XOR is its own inverse

If you XOR something with the same value twice, you get the original value back.

ciphertext = plaintext XOR key
plaintext  = ciphertext XOR key

Because of this, encryption and decryption often use the same operation — a property heavily used in CTR and GCM modes.

2. XOR mixes bits while keeping everything reversible

XOR doesn’t destroy information; it just combines two bitstreams. As long as the key or keystream is unpredictable, the output looks random.

Example

P = 10110011
K = 01100101
C = P XOR K = 11010110

Decrypting is the exact same process:

C XOR K = 11010110 XOR 01100101 = 10110011 = P

As you’ll see later in the post, this symmetry is what enables so many encryption modes to work.

Modes of Operation

So we have established that block ciphers are a form of symmetric encryption that takes a fixed-size input block and produces an output block of the same size. For example, a cipher might operate on a 128-bit block of data. But what if the data you want to encrypt is larger than the cipher’s block size? How do we encrypt a multi-gigabyte file or a continuous network stream?

A mode of operation is the specific approach we take to apply a block cipher on data larger than a single block. The choice of mode has significant implications for the security and performance of the encryption system. There are several of them but I’ll only cover four in this post: ECB, CBC, CTR, and GCM modes.

Electronic Code Book (ECB) Mode

ECB is the most straightforward and simplest, but also the most insecure mode of operation. The message is partitioned into blocks of the cipher’s fixed size, and each block is encrypted independently using the same key. Decryption is simply the inverse of the encryption using the same key.

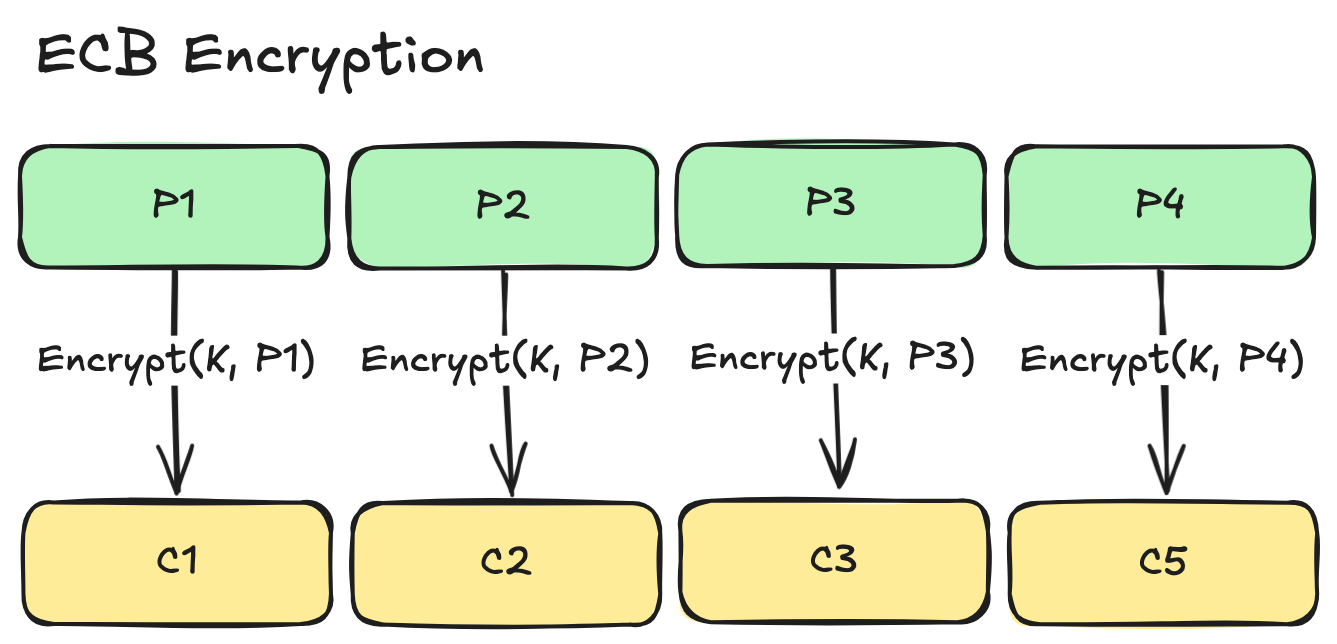
Because each block is independently encrypted from the other blocks, the mode is highly parallelisable across multiple CPUs for both encryption and decryption. However, there is a critical flaw in this mode’s design. Since the block ciphers are deterministic (meaning that for a fixed key K and fixed input block P, the output block is always the same), it leaks structural patterns of the plaintext into the ciphertext. This significantly increases the chance of attackers successfully analysing and deriving the plaintext, rendering the mode useless for any real-world use.

Cipher Block Chaining (CBC) Mode

The CBC mode addresses the primary flaw of ECB by introducing a “chain” between the adjacent blocks. The main idea is to mix up the plaintext block with some random bits in order to eliminate the repeating structural patterns in the ciphertext. To do this, it introduces an initialisation vector (IV)—a block with randomly initialised bits—and performs a XOR operation with the first plaintext block (P1). The resulting block (R1) is then encrypted to produce the first ciphertext block (C1). For all subsequent blocks, the plaintext block is XORed with the previous ciphertext block before being encrypted. This process is continued, linking each block to the one before it, until it encrypts all the data blocks.

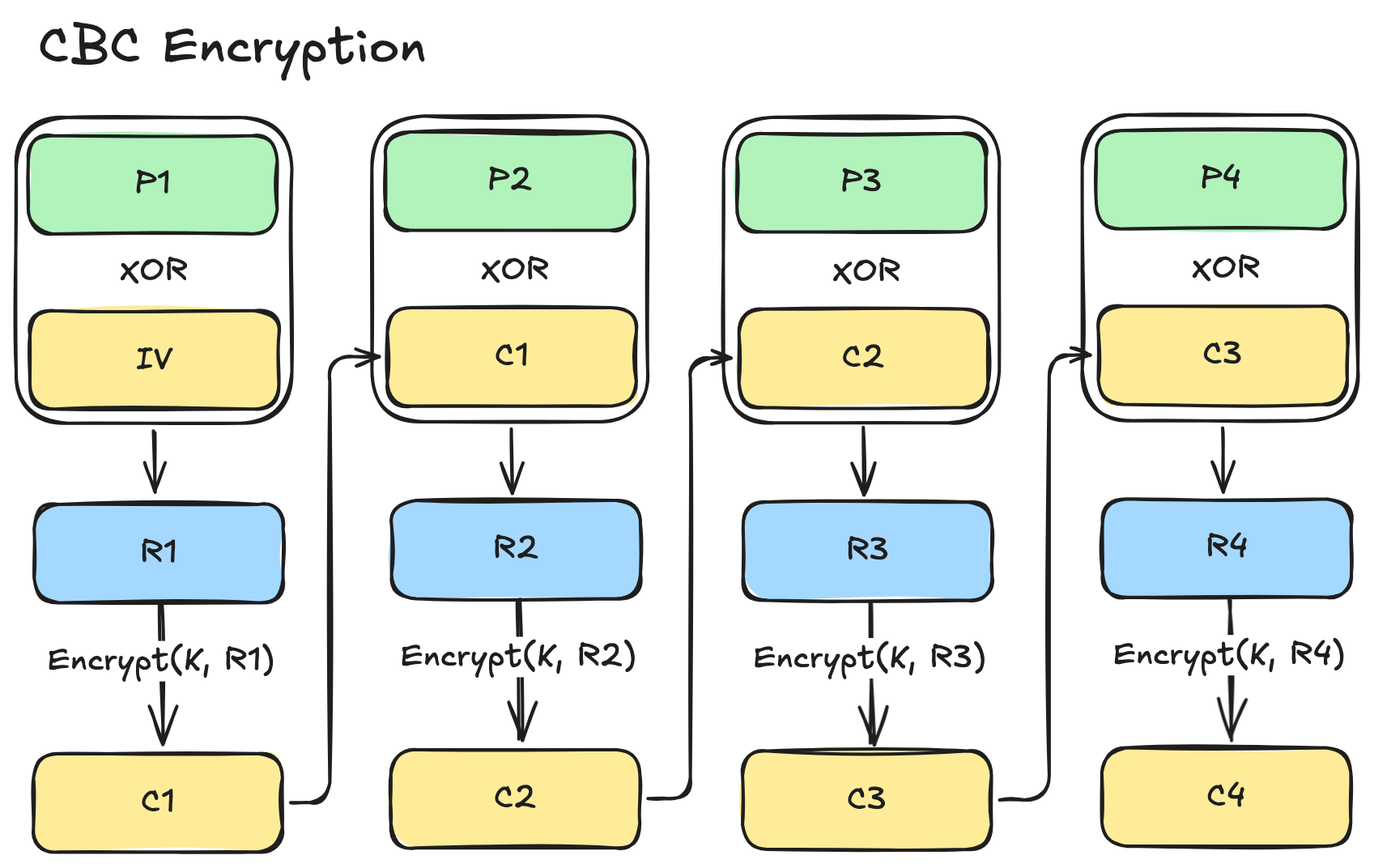
The decryption process is the inverse process as shown in the illustration below.

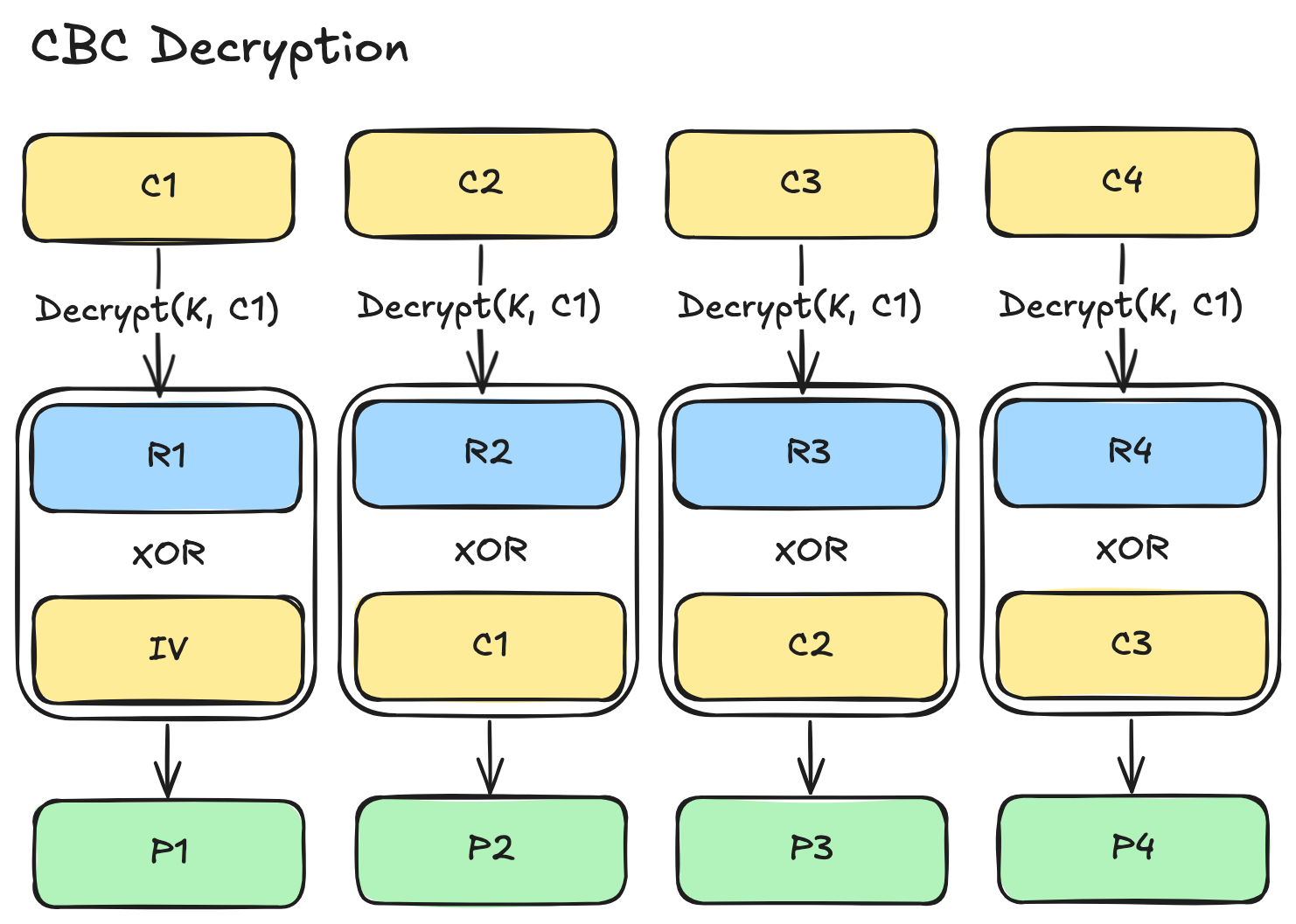
While CBC effectively hides patterns and produces much more secure ciphertext than ECB, it comes with several important limitations that have made it increasingly outdated in modern systems:

• Sequential Encryption: Encryption must occur strictly in order, block by block. Because each plaintext block depends on the previous ciphertext block, CBC cannot be parallelised for encryption. This makes it slower on modern multi-core systems and less suitable for high-throughput or low-latency applications. Decryption, however, can be parallelised.

• Limited Random Access: CBC does not support random-access encryption. You cannot encrypt block P_n without having encrypted blocks P₁ to P_n−1. This makes CBC unsuitable for use cases such as disk encryption or scenarios where only a small part of the data needs to be re-encrypted.

• Padding Required: CBC can only operate on full-size blocks, so the final block of plaintext must be padded. Historically, incorrect handling of padding has led to serious vulnerabilities such as padding-oracle attacks.

• IV Handling Is Critical: CBC requires a fresh, unpredictable IV for every encryption operation with the same key. Reusing an IV, or deriving predictable IVs, can completely break the security of the scheme.

Counter (CTR) Mode

The modes I have described so far apply encryption directly or indirectly on the plaintext blocks to produce ciphertext blocks and that makes intuitive sense. But the CTR mode is an interesting one because it takes a completely different approach. Instead of applying the encryption function on the plaintext block, it encrypts the incrementing counter together with a nonce—a unique, unpredictable bitstring—to generate a stream of psuedorandom bits called a keystream.

# Generate keystream blocks
# Note that `||` denotes bit concatenation
K1 = encrypt(nonce || 1)
K2 = encrypt(nonce || 2)
K3 = encrypt(nonce || 3)
Kn = encrypt(nonce || n)

This keystream is then XORed with the plaintext to produce the ciphertext.

C1 = P1 XOR K1
C2 = P2 XOR K2
C3 = P3 XOR K3
Cn = Pn XOR Kn

Now, take a moment to think about the benefits or implications of this keystream.

As you generate the keystream by encrypting the nonce and the counter, you can take any number of its bits and XOR with the bits from the plaintext (considering they are at the same bit position) to produce the ciphertext. You can XOR them bit by bit, a byte by byte, or in 16 byte chunks—it doesn’t matter. The CTR mode essentially turns the block cipher into a stream cipher.

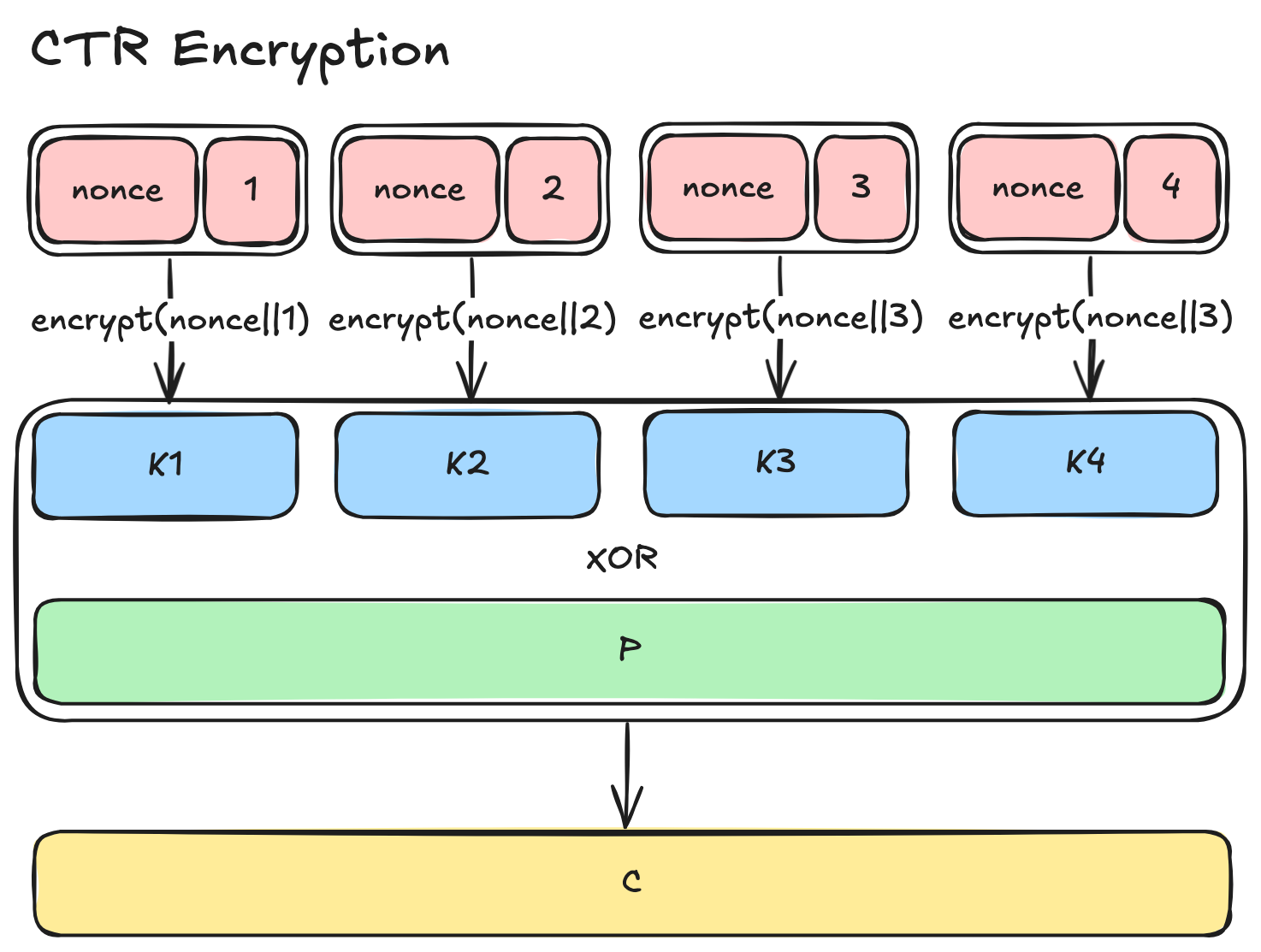
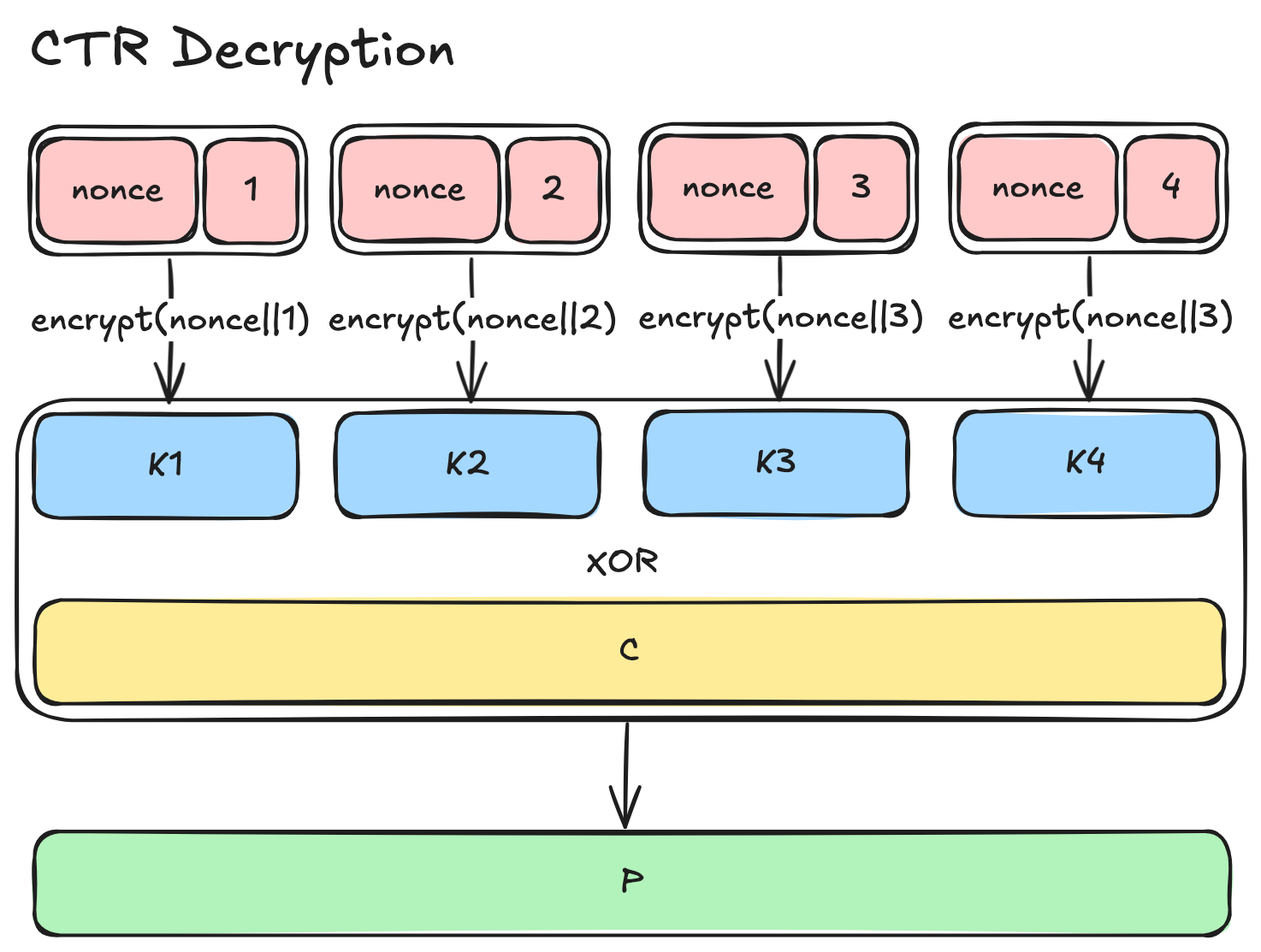
The CTR mode offers several advantages over CBC:

• Parallelisable: Each keystream block is independent because it is derived solely from the nonce+counter. That means both encryption and decryption can be parallelised easily across multiple CPUs.

• No Padding Required: CTR operates like a stream cipher and can encrypt arbitrary-length messages without padding.

• Random Access Friendly: Because each block depends only on the counter, you can jump directly to block N without processing the earlier blocks. This makes CTR mode popular for disk encryption and applications where partial reads/writes are common.

However, CTR mode also comes with a critical requirement: You must never reuse the same nonce+key pair. Doing so would cause keystream reuse, allowing attackers to XOR two ciphertexts together and recover information about both plaintexts. Aside from that, CTR itself provides no authentication or integrity guarantees, so it is usually paired with a MAC, or used inside authenticated modes such as GCM.

Galois/Counter (GCM) Mode

We finally arrive at the GCM mode. It is one of the most widely used modes today. It builds directly on the CTR mode for its encryption process, meaning that it inherits all of CTR’s strengths such as parallelism, no padding, and random-access support, but adds a powerful integrity mechanism on top. This makes GCM what’s called an AEAD (Authenticated Encryption with Associated Data) mode: it provides both confidentiality (encryption) and authenticity (tamper detection) in a single operation. Basically, GCM is CTR mode with integrity and authenticity guarantees.

Like CTR, GCM encrypts plaintext by encrypting nonce+counter values to produce a keystream, which is XORed with the plaintext. What sets GCM apart is the addition of a GHASH function, which operates over a “finite field”. GHASH takes the key, ciphertext and optional associated data (AAD)—such as headers in network protocols—and computes an authentication tag. This tag ensures that any modification to the ciphertext or AAD is detectable during decryption.

The benefits of GCM include:

• Authenticated Encryption: You get both encryption and integrity in one step. If any part of the data is tampered with, decryption fails and the system rejects the message.

• High Performance: GCM is extremely fast and highly parallelisable. Modern CPUs often include dedicated instructions (like Intel’s AES-NI) that accelerate both AES and the GHASH computation, making AES-GCM the default choice in TLS, SSH, and many other protocols.

• No Padding Required: Like CTR, GCM works on arbitrary-length messages without padding.

• Supports Associated Data: You can authenticate metadata—such as protocol headers—without encrypting it.

As with CTR mode, the nonce in GCM must never be reused with the same key. GCM is especially sensitive to nonce reuse; reusing a nonce can lead to catastrophic key recovery attacks. When implemented correctly, however, GCM offers both strong security guarantees and excellent performance, making it the de facto encryption mode for secure communication today.

Nonce vs. IV

Before I get to the summary, I want to clarify the difference between a nonce and an IV, because they look similar but serve different purposes. The key idea for a nonce is uniqueness. It doesn’t need to be random, but it must never repeat when used with the same key. Reusing a nonce in counter-based modes (like CTR or GCM) causes the keystream to repeat, which leads to catastrophic failures such as the two-time pad vulnerability. This is explained in the next part of the series.

Meanwhile, the key idea for an IV (initialisation vector) is unpredictability. In chaining modes such as CBC, the IV is XORed with the first plaintext block before encryption. If the IV can be predicted ahead of time, attackers can exploit this to perform chosen-plaintext attacks and infer structural information about the first block. The IV does not need to be unique, but using random IVs typically makes them unique in practice.

Summary

In this first part of the series, we explored the foundations of modern cryptography—how ciphers work, why security depends on keys rather than hidden algorithms, and the difference between symmetric and asymmetric encryption. We also looked at stream ciphers, block ciphers, and how block ciphers use modes of operation to securely handle data of any size. Finally, we introduced four important modes—ECB, CBC, CTR, and GCM—highlighting why GCM has become the modern standard for fast, authenticated encryption.

In the next part, we’ll take these ideas and apply them to real-world systems, exploring AES-GCM in practice and using AWS KMS to perform encryption using envelope encryption.

References

• Schneier, Bruce. Applied Cryptography: Protocols, Algorithms, and Source Code in C (20th Anniversary Edition). Wiley, 2015.
• “Modes of Operation – Computerphile.” https://www.youtube.com/watch?v=Rk0NIQfEXBA (accessed 14 Nov 2025).